本文翻译自 A note on standard deviation ,解释了让大部分统计学入门者感到困惑的一个经典问题。
假如你正同时上几门课并且刚刚通过考试拿到成绩。很自然的,我们想了解班里其他学生的情况好让你的成绩有个参照。平均值或中位数可以告诉我们所有成绩的“中心值”或者“中间数”,但是它们很难体现成绩的分布或者变化。
我们来看一个小例子。假如5名学生参加三门课程获得的成绩如下:
| 课程1 | 课程2 | 课程3 |
|---|---|---|
| 82 | 82 | 67 |
| 78 | 82 | 66 |
| 70 | 82 | 66 |
| 58 | 42 | 66 |
| 42 | 42 | 65 |
每一个课程都有一个平均值,\(\overline{x}\),且都为66,尽管如此,不同课程成绩的波动仍然有很大的差异。对这种波动的测量的其中一种方法是极差,也就是最大值与最小值之差。本例中,前两门课程极差均为82-42=40而第三门课程极差为67-65=2。因为课程1和课程2有相同的极差但是它们的偏差明显不同,所以极差不是一个测量偏差的理想指标。我们还可以这样看待偏差,课程3中所有的成绩都和平均值比较接近,课程1中有些接近而有些远离,课程2中所有成绩都远离均值。按照这样的观点我们可以引入标准差的概念。
首先来看看课程1,对每个学生计算其成绩与平均分的差值。
| 课程1 | \(x_1-\overline{x}\) |
|---|---|
| 82 | 16 |
| 78 | 12 |
| 70 | 4 |
| 58 | -8 |
| 42 | -24 |
这些差值的平均可以计算得到并作为对偏差的一种度量方式,在此例中其值为0。我们真正需要的其实是每个分数与均值之间的距离。你可以对差值取绝对值再平均,称之为平均差(mean deviation),即\(md=\frac{\sum|x_1-\overline{x}|}{n}\),n为课程的学生数。对课程1而言\(md=\frac{64}{5}=12.5\)。另一种处理负差值的方式就是取平方相加。
| 课程1 | \(x_1-\overline{x}\) | \((x_1-\overline{x})^2\) |
|---|---|---|
| 82 | 16 | 256 |
| 78 | 12 | 144 |
| 70 | 4 | 16 |
| 58 | -8 | 64 |
| 42 | -24 | 576 |
第三列的和为1056。为了求得标准差s,将该和除以n-1并开方。课程1的方差则为\(s=\sqrt{\frac{\sum(x_1-\overline{x})^2}{n-1}}=\sqrt{\frac{1056}{4}}=16.2\)
同样可以计算得到课程2和课程3方差分别为21.9和0.7。课程3分数都靠近均值因此方差非常小;课程1分数分布在42和82之间,方差也相当可观;课程2分数都远离均值,方差因此更大。方差是统计学家最常用的测量数据集偏差的量。
我们需要对分母采用n-1做出一个解释。为此我们换一个例子。假设我对北美中学生每天花在数学作业上的时间感兴趣。这里总体就是所有北美的中学生,数目非常大。设人数为N,我真正的兴趣在于这个总体的均值和方差。统计学家习惯于用希腊字母表示总体的量,因此总体均值记为\(\mu=\frac{\sum x_1}{N}\),类似的方差为\(\sigma=\sqrt{\frac{\sum(x_1-\mu)^2}{N}}\)。注意这里分母为N。
统计学家通常只选择一个样本,比如n个学生,在这个小数据集上估计\(\mu\)和\(\sigma\),而不是直接对这么大的总体进行统计。这里n可能是25,30或100或者甚至1000,不过它肯定远小于N。为了估计\(\mu\)很自然地我们可以用样本均值\(\overline{x}\)。同样的为了估计\(\sigma\)似乎用\(\sqrt{\frac{\sum(x_1-\overline{x})^2}{n}}\)也很合理,不过这样计算往往会“低估”\(\sigma\),尤其是在n比较小的时候。由于这个以及其它技术原因,通常\[s=\sqrt{\frac{\sum(x_1-\overline{x})^2}{n-1}}\]被用来估计\(\sigma\)。
如果你有计算器可以直接计算方差的话你可以试着找出它使用的是哪种计算方法。用一个3个数字的数据集-1,0,1,用手工和计算器的方式分别计算方差,看看计算器使用的是哪种计算方法吧。
译者注:该文章在网上发表后,有老师希望文章作者对n与n-1的选择问题作出更详尽的解释,本文作者回复邮件称可以用一个小实验来进行验证。这里把回复邮件也做了个简单的翻译:
与其对我所说的“其它技术原因”做一个理论上精巧的阐述,我更愿意建议你和你的学生做一个实验以说明“这个数值往往低估了\(\sigma\)值”以及“其它技术原因”是什么。我将在下面的讲述中针对\(\sigma^2\),而非\(\sigma\)。
我们用白豆和黑豆来进行实验。你可以用任何除了使用视觉外难以区分的物体来模拟。你可能需要60到100个这样的物件,其中1/4作为白豆,3/4作为黑豆。假定每个白豆取值为5,黑豆取值为1。这样总体就设置好了。整个总体的比例以及均值、方差都应当向你的学生保密直到实验完成。很简单的,总体的均值为:\[\mu=1(\frac{3}{4})+5(\frac{1}{4})=2\]方差为:\[\sigma^2=(1-2)^2(\frac{3}{4})+(5-2)^2(\frac{1}{4})=3\]
学生的任务是要利用一个随机的测试样本来估计豆子的均值及方差。为了让计算保持简单我建议样本数目设为n=3。把豆子放在一个学生无法看到但是可以取出的地方,比如一个袋子或者一个瓶子里,每个人每次随机取出3颗豆子并做样本记录。每个学生记录完后应当将豆子放回。如果你能得到50到60个样本那就最好了,这样你就可以让每个学生选择两个样本并且独立地处理它们。每个学生应当计算他的样本的均值以及方差,并且要计算(方差)两次,一次除以n,一次除以n-1。把学生交给你的结果汇总记录在三栏里面,一栏为均值,一栏为除以n得到的方差,另一栏为除以n-1得到的方差。你会发现均值一栏只有四种不同的数值,其它两栏都只有两种不同的值。这是由于样本值n=3选得比较小的缘故。如果样本值大一点那么每栏可能值得数目就会多一点。
我们首先考虑第一栏,即均值。该栏里的每一个数值都是对总体均值的一个估计。现在告诉学生们总体的均值这样他们就可以看到有些估计值太大而另一些太小。再计算该栏所有值的均值。这个均值应当很靠近2,也就是总体的均值。从理论上说,“平均而言”,样本均值和总体均值是相等的。我们把这样的性质称之为无偏,样本均值就是总体均值的一个无偏估计。
现在考虑第二和第三栏,计算它们的均值并告诉学生们总体的方差。除以n-1得到的方差的均值应当很接近总体的方差而另一栏的均值就会小得比较多。样本方差(除以n-1)是总体方差的一个无偏估计。样本方差(除以n)是总体方差的一个有偏估计,并且“总是低估\(\sigma\)”。
最后一点。当分母为n-1时计算出来的值为总体方差的一个无偏估计。有没有可能存在一个比样本方差更好的对总体方差的估计值呢?你不仅仅希望这个新的估计值是无偏的而且还希望在该栏的所有的新的估计值大部分都接近总体方差。也就是说,你希望新的估计值的方差要小。这是我所说的用样本方差来估计总体方差的“其它技术原因”之一。在所有你可以使用的合理的估计当中,样本均值有着最小的方差。
希望这个建议能有帮助。如果你做了这个实验,请告诉我结果如何。
有博士生做了本文作者建议的实验并且给出了excel表格,部分截图如下:
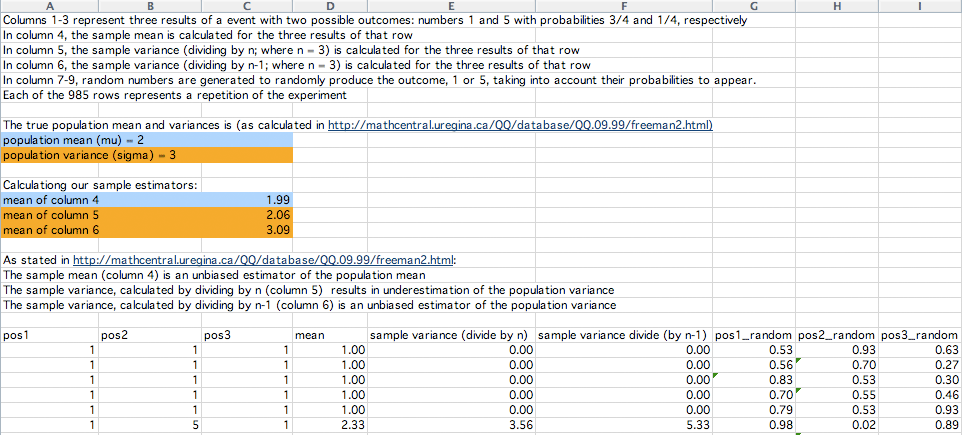
补充:实际上n和n-1的选择问题用数学理论很容易解释,那就是n-1时样本方差的期望值就是总体方差(对样本方差求期望,简单推导即可得到)。造成大部分人困惑的原因就是n-1没有n看上去那么自然,同时对于总体和样本的概念以及它们的地位有所混淆。这篇文章其实讲的很浅显,但是国外教授对于简单问题往往会给出大量的篇幅,这与国内教材动辄大篇数学公式的风格大不一致。我们不能简单地说两种模式孰高孰低,但是国人受到苏联模式的影响如此深远,却始终成不了数学大国,恐怕是时候改变下思路了。